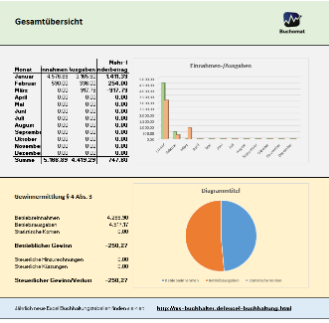
Break Even Point Rechner
Gewinnschwelle berechnen: Formel, Beispiel + Gratis-Rechner
Inhaltsverzeichnis
Definition Break-Even-Point, Formel + Beispiel
Die Gewinnschwelle (auch bekannt als Break-Even-Point) ist der Punkt, an dem die Gesamtkosten eines Unternehmens gleich den Gesamteinnahmen sind und somit weder ein Gewinn noch ein Verlust erzielt wird. Um die Gewinnschwelle zu berechnen (siehe auch Break-Even-Rechner), müssen Sie die festen Kosten und die variablen Kosten Ihres Unternehmens kennen.
Definition: Als Break-Even-Point wird die Gewinnschwelle bzw. der Kostendeckungspunkt bezeichnet.
Also der Punkt an dem die Erlöse die Kosten abdecken und der Verlustbereich verlassen bzw. der Gewinnbereich beginnt. Die Break Even Point Formel stellt die Fixkosten zuzüglich variabler Stückkosten mit der abgesetzten Menge x Verkaufserlösen/ Stück gegenüber. Das Ergebnis ist die verkaufte Produktmenge, die mit ihrem Deckungsbeitrag die Fixkosten übersteigt. Deutsche Bezeichnungen: Gewinnschwellenanalyse, Nutzenschwellenanalyse, Deckungspunktanalyse.
Die Formel für die Gewinnschwelle lautet:
Gewinnschwelle = feste Kosten / (Verkaufspreis pro Einheit - variable Kosten pro Einheit)
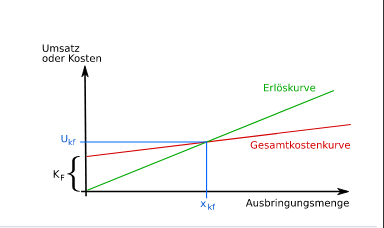
In der grafischen Darstellung entspricht der Anstiegswinkel der Gesamtkostenkurve den variablen Stückkosten. Der Anstiegswinkel der Umsatzkurve entspricht dem Stückerlös. Ein Umsatz unterhalb des Deckungspunktes führt zu einem Verlust, ein Umsatzvolumen größer als der Deckungspunkt bedeutet Gewinn. Der Deckungspunkt ist dort erreicht, wo die Deckungsbeitragskurve die Kurve des Fixkostenblocks schneidet. Jede verkaufte Leistungseinheit oberhalb des Deckungspunktes steigert den Gewinn in Höhe des Stückdeckungsbeitrags. Unterhalb des Deckungspunktes entsteht mit jeder weniger abgesetzten Leistungseinheit ein Verlust in Höhe des Stückdeckungsbeitrags.
Beispiel: Angenommen, Ihr Unternehmen hat feste Kosten von 50.000 Euro pro Jahr, einen Verkaufspreis von 10 Euro pro Einheit und variable Kosten von 6 Euro pro Einheit. Sie können die Gewinnschwelle wie folgt berechnen:
Gewinnschwelle = 50.000 / (10 - 6) = 12.500 Einheiten
Das bedeutet, dass Sie 12.500 Einheiten Ihres Produkts oder Ihrer Dienstleistung verkaufen müssen, um die Gewinnschwelle zu erreichen und weder einen Gewinn noch einen Verlust zu erzielen. Wenn Sie mehr als 12.500 Einheiten verkaufen, erzielen Sie einen Gewinn. Wenn Sie weniger als 12.500 Einheiten verkaufen, erleiden Sie einen Verlust.
Die Break-even-Analyse ist ein einfach handhabbares Tool zur Unterstützung betriebswirtschaftlicher Entscheidungen unter Berücksichtigung von Umsatz und Kostenstrukturen. Sie ermöglicht die Darstellung der strukturellen Rentabilitätszusammenhänge des Unternehmens und seiner Produkte. Der Break-Even-Point ist ein wichtiger Indikator für Unternehmen, da er ihnen hilft, die Rentabilität ihrer Produkte oder Dienstleistungen zu verstehen und ihre Geschäftsstrategie entsprechend anzupassen.
Top Break-Even-Point
Wie berechnet man den Break-Even-Point?
Der Break-Even-Point ist also der Punkt, an dem die Einnahmen die Ausgaben genau decken. Dies bedeutet, dass das Unternehmen keinen Gewinn und keinen Verlust macht. Der Break-Even-Point wird in der Regel als eine bestimmte Anzahl von Einheiten berechnet, die verkauft werden müssen, um die Kosten des Unternehmens zu decken. Er kann auch in Bezug auf Umsatz oder sogar Zeit berechnet werden.
Wie viel müssen Sie verkaufen, um Gewinn zu machen? Die Antwort darauf liefert Ihnen dieser kleine Break Even Point Rechner. Mit dem Break-Even-Rechner können Sie herausfinden, wie viel Stück eines Produkts Sie absetzen müssen, um Gewinne zu erzielen. Im Break-Even-Point entsprechen die erzielten Erlöse dabei genau der Summe aus den Fixkosten und den variablen Kosten.
Break-Even-Point berechnen
Tipp: Businessplan Vorlage (PDF) zum kostenlosen Download
Die Break-even-Analyse bestimmt dasjenige Absatzvolumen eines Unternehmens, bei dem die Vollkosten gedeckt sind. Nach Deckung der Vollkosten gelangt das Unternehmen in die Gewinnzone. Der Break-even-Punkt (Deckungspunkt) kann in EUR (Umsatz), in Leistungseinheiten (Ausbringung) oder in Zeiteinheiten angegeben werden.
Der Break-Even-Point (BEP) kann auf verschiedene Arten berechnet werden, je nachdem, welche Informationen verfügbar sind.
Die häufigste Methode zur Berechnung des BEP ist die Verwendung der Formel:
BEP (in Einheiten) = Fixkosten / (Verkaufspreis pro Einheit - Variable Kosten pro Einheit)
Die Fixkosten sind die Kosten, die das Unternehmen hat, unabhängig von der Anzahl der produzierten oder verkauften Einheiten. Beispiele für Fixkosten sind Miete, Gehälter, Versicherungen usw.
Die Variable Kosten sind die Kosten, die sich direkt auf die Anzahl der produzierten oder verkauften Einheiten auswirken. Beispiele für variable Kosten sind Materialkosten, Löhne für die Herstellung der Einheiten usw.
Der Verkaufspreis pro Einheit ist der Preis, zu dem das Unternehmen die Einheiten verkauft.
Wenn man die oben genannte Formel anwendet, erhält man die Anzahl der Einheiten, die das Unternehmen verkaufen muss, um die Fixkosten zu decken.
Eine andere Methode ist die Berechnung des BEP in Bezug auf den Umsatz.
Der Break-even ist demnach erreicht, wenn der Umsatz den Kosten entspricht oder anders ausgedrückt: der Break-even ist erreicht, wenn der Deckungsbeitrag den Fixkosten entspricht.
Der Deckungspunkt wird rechnerisch durch die Gleichung E = GK bzw. P * X = FK + VK * X
Daraus ergibt sich als Deckungsausbringung (kritische Stückzahl): X (kritisch) = FK/P - VK bzw. X (kritisch) = FK / DB
E = Erlös (Umsatz)
GK = Gesamtkosten
P = Verkaufspreis
X = Verkaufsmenge (Stückzahl)
VK = variable Kosten
FK = Fixkosten
DB = Stückdeckungsbeitrag
Durch Umformung und Auflösung der Ausgangsgleichung lassen sich mit der der Break-even-Analyse weitere Fragestellungen beantworten.
- Bei welcher Kapazitätsauslastung werden Verluste erwirtschaftet?
- Welche Auswirkungen haben Absatzschwankungen auf den Gewinn?
- Ab wann werden die Abschreibungen nicht mehr erwirtschaftet?
- Bei welchem Absatzvolumen gibt es Cash-flow-Defizite?
- Wie wirken sich Veränderungen der Preise auf die Rentabilität aus?
- Welcher Umsatz ist erforderlich, um einen Mindestgewinn zu erzielen?
- Wie wirken sich Veränderungen der Kosten auf die Rentabilität aus?
- Welcher Mehrumsatz ist erforderlich, um bestimmte Mehrkosten zu decken?
Tipp: Preisuntergrenze berechnen.
Top Break-Even-Point
Wie berechne ich den Break-Even-Point in Excel?
Es gibt mehrere Möglichkeiten, den Break-Even-Point (BEP) in Excel zu berechnen. Eine Möglichkeit besteht darin, eine Tabelle mit den notwendigen Daten zu erstellen und dann die Formel in eine Zelle einzugeben. Hier ist ein Beispiel für eine einfache Berechnung des BEP in Excel:
-
Erstellen Sie eine Tabelle mit den Spalten "Einheiten verkauft", "Verkaufspreis pro Einheit", "Variable Kosten pro Einheit" und "Fixkosten".
-
Geben Sie die Daten in die entsprechenden Zellen ein.
-
Geben Sie die Formel =SUM(Fixkosten) / (SUM(Verkaufspreis pro Einheit) - SUM(Variable Kosten pro Einheit)) in eine Zelle ein. Diese Formel berechnet die Anzahl der Einheiten, die verkauft werden müssen, um die Fixkosten zu decken.
-
Ziehen Sie die Formel auf alle Zellen der Tabelle, um die Berechnung für jede Verkaufseinheit durchzuführen.
Eine andere Möglichkeit wäre es, ein Diagramm zu erstellen und die Daten darauf zu plotten, um visuell zu sehen, wann die Kosten und die Einnahmen sich die Waage halten.
Es gibt auch vorgefertigte Excel-Vorlagen für die Berechnung des BEP, die Sie verwenden können, um die Berechnungen schneller durchzuführen.
Es ist wichtig zu beachten, dass die Berechnung des BEP nur ein Indikator für die Rentabilität.
Top Break-Even-Point
Noch mehr hilfreiche Steuerrechner

 Steuer-Newsletter.
Steuer-Newsletter.